Posts
Using categorical logic for AI planning
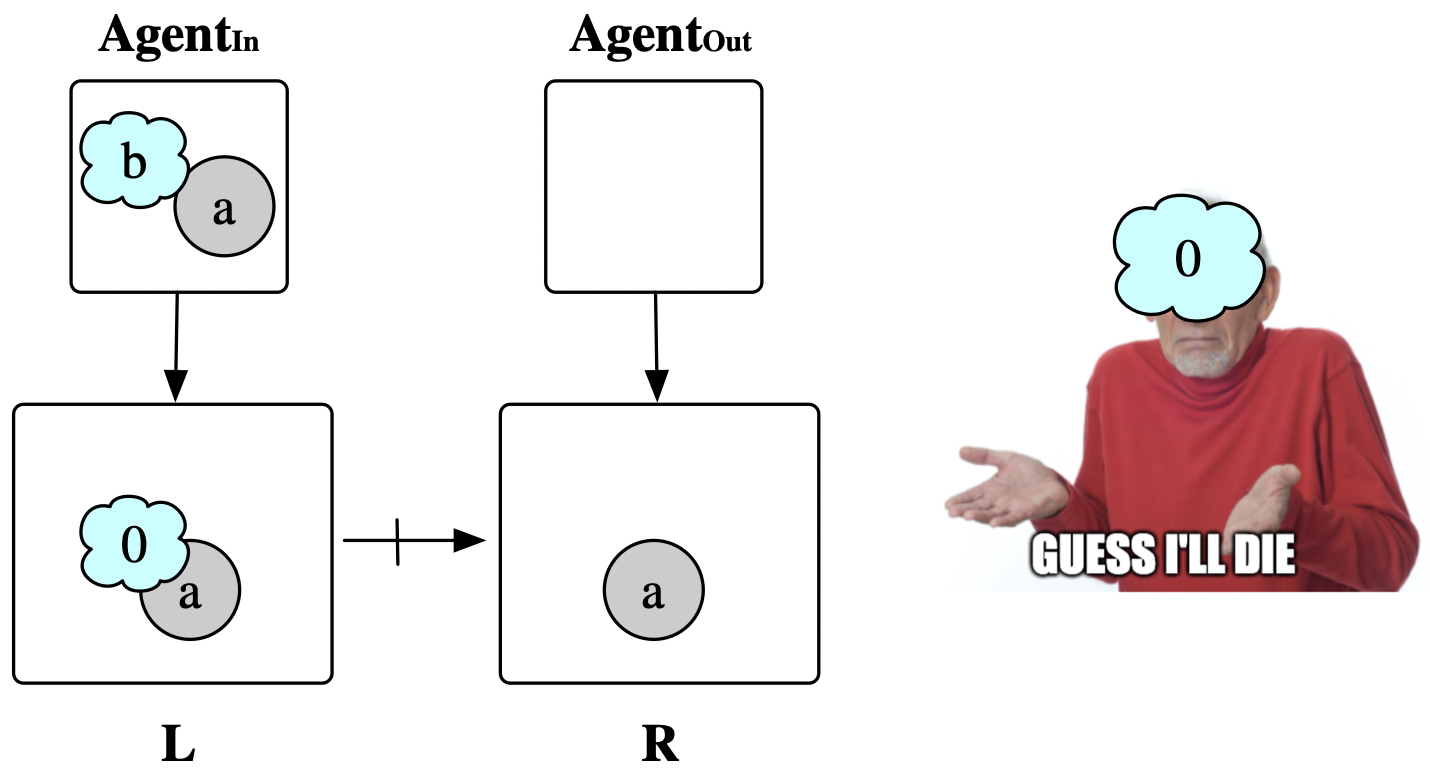
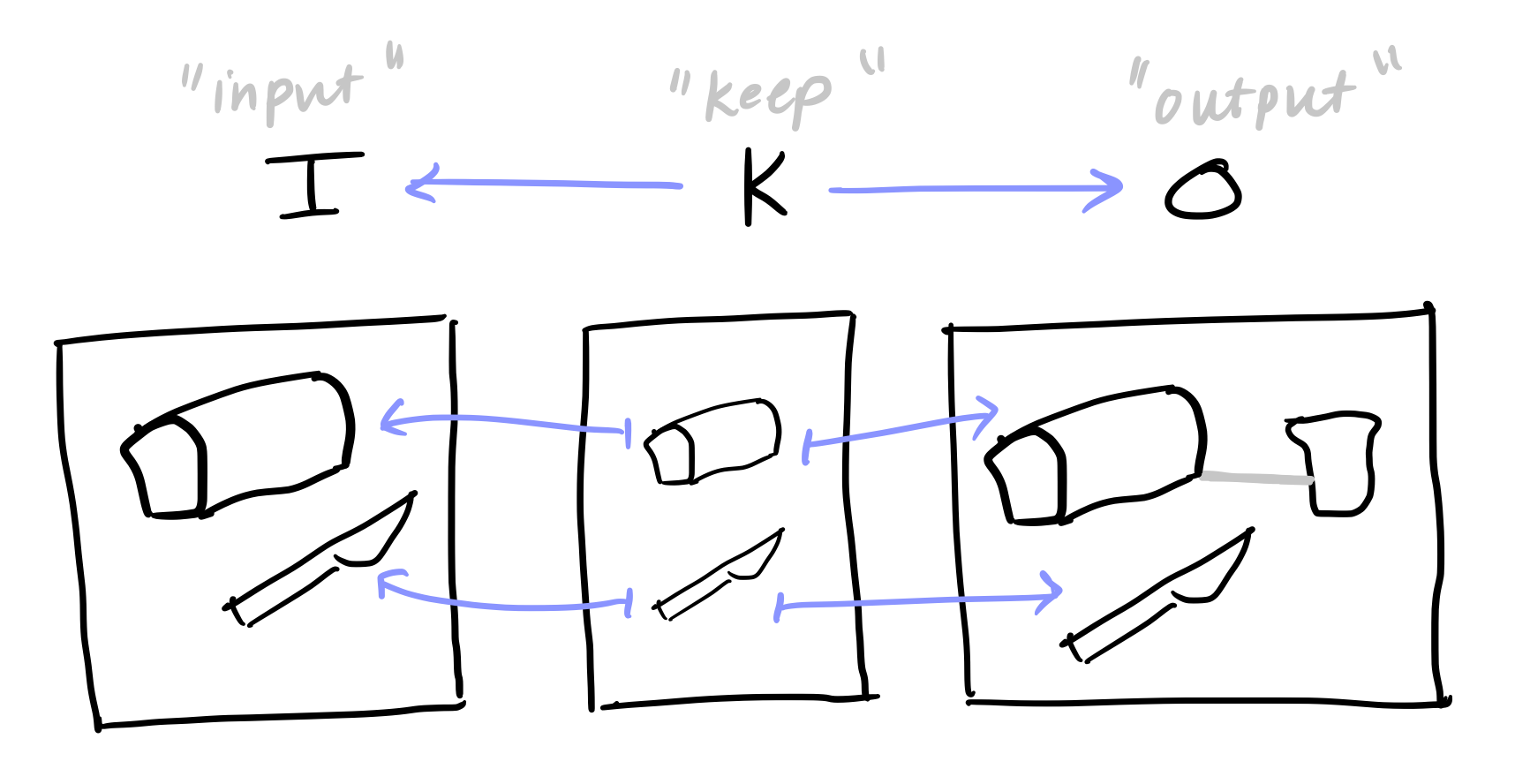
It’s breakfast time! You wake up and walk to your kitchen and notice a loaf of bread, a knife, a raw egg (in its shell), a skillet, and a stove burner sitting on the counter. You’re hungry and your preferred state of existence is to, instead, have an egg sandwich sitting on your counter. You are saddened by the situation, but feel empowered to change it! You compare what you have and what you want, recall what cooking skills you have, and devise the following steps:
Equality vs equivalence: computing isomorphism classes of C-sets
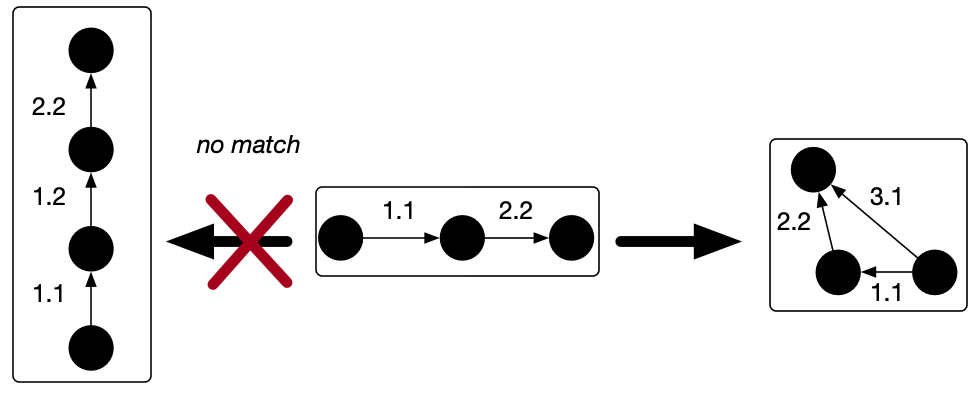
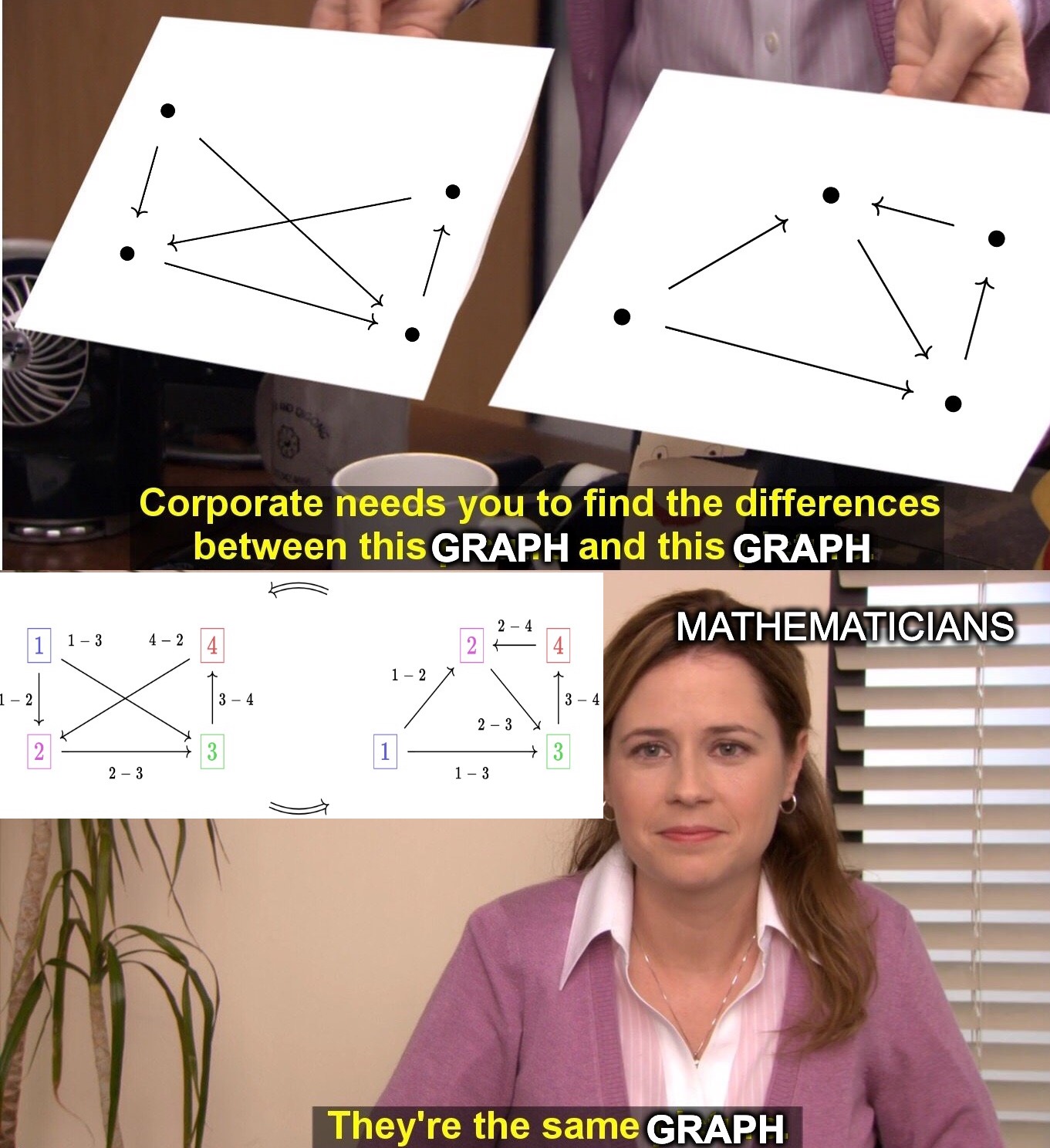
For graphs and C-sets more generally, the most useful notion of equivalence differs from strict equality of the underlying data structures. Finding automorphism classes of C-sets addresses this problem; we explore how to compute automorphism classes and applications of them.
Graphs and C-sets IV: The propositional logic of subgraphs and sub-C-sets
Nonclassical logics are often thought to be abstruse and exotic, but they arise naturally as the logic of connected spaces. In this post, we introduce the propositional logic of subgraphs, and more generally of sub-C-sets, and illustrate it with computational examples. The nonclassicality of this logic is seen to be not just natural but inevitable, and also surprisingly useful.
Graphs and C-sets III: Reflexive graphs and C-set homomorphisms
Reflexive graphs are graphs where every vertex has a distinguished self-loop. While this may seem inconsequential, reflexive graphs have interestingly different properties than ordinary graphs owing to their different morphisms. We will see that reflexive graphs are more geometrical than graphs and also review the general notion of homomorphism between C-sets.
Composing open dynamical systems II: Undirected composition
In the previous post, we defined a general approach for composing dynamical systems based on the mathematics of operads and operad algebras. In this post, we explore an undirected composition syntax in which dynamical systems compose by sharing resources. We also get a taste of hierarchical composition, i.e. composing systems which are themselves composites.
Composing open dynamical systems I: Directed composition
Informally, many models are specified as compositions of primitive dynamical systems. In this series of posts, we make this modular specification formal by introducing a computing framework from composing open dynamical systems. In this first post of the series, we examine directed theories for composition.
C-sets for data analysis: relational data and conjunctive queries
Not just useful for graphs, C-sets are a general-purpose tool for data analysis offering the functionality of an in-memory relational database. In this post, we illustrate Catlab’s new capabilities for querying C-sets and we explain the categorical underpinnings of conjunctive queries.
Compositional epidemiological modeling using structured cospans, part 2
Following up the original post, we explain how modeling is simplified by a shift in perspective from composing structured cospans in categorical style to composing structured multicospans in operadic style.
A categorical approach to scientific data management
We present an approach to scientific data management that utilizes category theory to seamlessly integrate workflow creation, database generation, and database querying. We use Catlab as a backend to provide this more continuous and consistent database experience.
Compositional epidemiological modeling using structured cospans
Structured cospans are a categorical method for turning closed systems into open ones. We show how structured cospans of Petri nets can be used to construct complex epidemiological models in a compositional way.
The categorical scoop on attributed C-sets
In this post we unveil the category of attributed C-sets. It is an upgrade to the category of C-sets that makes each element of a component set (e.g. each vertex or edge in a graph) have attributes, which may be elements of arbitrary sets/Julia types. In order to formalize attributed C-sets, we also take a tour of double category theory and profunctors.
Graphs and C-sets II: Half-edges and rotation systems
Graphs are made up of vertices and edges, but an important variation on this concept is based on “half-edges” or “darts.” We explain how half-edge graphs are implemented as C-sets in Catlab.jl and how they are used in topological graph theory to represent embeddings of graphs in surfaces.
Graphs and C-sets I: What is a graph?
Through the course of this blog we will encounter a diverse cast of algebraic structures generalizing the concept of a graph. In this post we start at the very beginning, with how category theorists understand graphs, how graphs are an example of a general class of structures called “C-sets,” and how C-sets can be used as data structures in Julia through Catlab.jl.