Using categorical logic for AI planning
$$
$$
This post is cross-posted at the Topos Institute blog.
”Engineers are not the only professional designers. Everyone [or thing] designs who devises courses of action aimed at changing existing situations into preferred ones.” – Herbert Simon (Simon 1988)
It’s breakfast time! You wake up and walk to your kitchen and notice a loaf of bread, a knife, a raw egg (in its shell), a skillet, and a stove burner sitting on the counter. You’re hungry and your preferred state of existence is to, instead, have an egg sandwich sitting on your counter. You are saddened by the situation, but feel empowered to change it! You compare what you have and what you want, recall what cooking skills you have, and devise the following steps:
- Slice the bread twice with a knife
- Put the slices of bread on a plate
- Put the skillet on the stove burner
- Crack the egg on the skillet
- Wait until the egg is cooked
- Put the egg on a slice of bread
- Close the bread
In this example, and in all planning problems, you can notice three conceptual notions: a plan, a planner, and a planning problem. The plan is the sequence of steps you devised. The planner is your cognitive reasoning activity. And the planning problem is the comparison of the states and the knowledge of skills you have. Planning is fairly automatic for most everyday tasks, so much so that we rarely think about these distinctions or even acknowledge that we’re doing any planning. However, if we wish to transition this activity to a computer, making all three concepts computable is necessary.
Automated planning is the domain of artificial intelligence (AI) aimed at identifying a sequence of actions, or a plan, that changes the current state of the world to a preferred state, namely one that meets some goal criteria. A planner takes a planning problem and produces a plan. One choice, the most common, is to construct a language syntax that can accommodate the semantics of actions, action requirements, and action effects. It’s then up to the planner to devise its own syntax and semantics for how to interpret, manage this information, and present a plan. For example, in practice, architectures that involve planning usually call on a PDDL planner (Ghallab et al. 1998) as an external service. The way they manage and update data about the world is handled independently by either translating the plan steps into database updates, or (more likely) re-sampling the world during or after the plan is executed. Evidently, having differing languages could result in conflicts and reduced inteoperability between planners, databases, and plan consumers.
Another choice would be to define a common abstraction, modeling for syntax and semantics, for the planner, planning problem, and the plan to reduce friction between representations. In this blog post, I will explain how a category-theoretic method called double-pushout (DPO) rewriting in the category of copresheaves can operationalize these concepts.
The anatomy of a rewrite rule
Rewrite rules are the atomic operations that translate data from one state to another. A rewrite rule contains three parts: an input, a keep, and an output. The input portion describes the types of things and relationships that are required before the rule can be applied to a world state. The output portion describes the types of things and relationships that exist in the world after the rule has been applied. The keep portion describes the types of things that remain consistent between the input and the output. For example, if we want to design a rule about slicing a piece of bread, we might want an input to contain a loaf of bread and a knife. At the end of this action, what we would want is a loaf of bread, a slice of bread, and a knife. We also want to say that the loaf of bread and knife we end up with is the same loaf of bread and knife we started with.
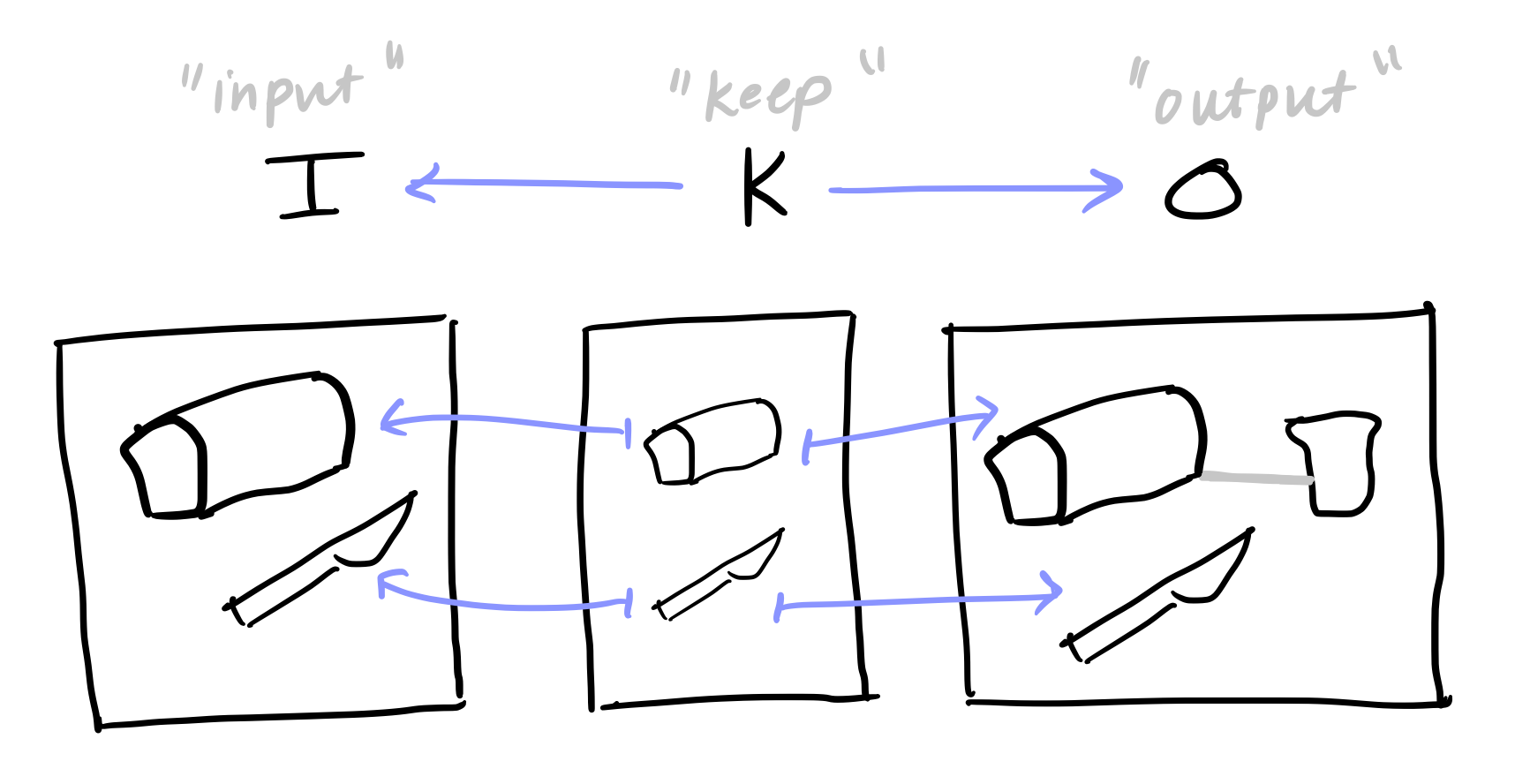
The terms “input” and “output” are intentionally reminiscent of pre-conditions and post-conditions/effects in the traditional planning literature. However, the term “keep” is a novel concept that was introduced to track entities that persist between the two states. “Why,” you might wonder, “can’t I just construct a map directly from the input to the output?” Interestingly, the keep portion gives us useful information about what elements have permission to disappear. If I had an element in the input that did not appear in the output, a map directly from the input to the output would force me to assign that element to something (assuming our maps are total) which would not be conceptually accurate. However, if it did not exist in my keep, then I would not need to account for it in my output state and it would be free to disappear. In automated planning, the frame problem is concerned with how to axiomatically account for information that remains unchanged. While this method does not exactly provide a set of axioms, it does provide a mechanism to declare what things remain unchanged when a rule is applied.
Now I’ve not said anything about the nature of the input, keep, and output portions of my rules. What are they? Graphs? Sets? Manifolds?! Well, formally, a rule is a span in the category of copresheaves, or \mathsf{C}-sets.
What are \mathsf{C}-sets?
Let \mathsf{C} be a small category, which we think of as a schema. A \mathsf{C}-set, also called a copresheaf on \mathsf{C}, is a functor from the schema \mathsf{C} to the category \mathsf{Set}. The schema is a category whose objects are types and whose morphisms describe “is-a” and other functional relationships between types. You can consider it to be a denotational semantics for ontologies. The category \mathsf{Set} is the category of sets and functions. Thus, a \mathsf{C}-set is a functor that sends types to sets and type relationships to functions. \mathsf{C}-sets are a simple model of categorical databases (Spivak 2012) and have a full-featured implementation in Catlab.jl (Patterson, Lynch, and Fairbanks 2021).
Morphisms of \mathsf{C}-sets are natural transformations between functors. With this definition, for any schema \mathsf{C}, there is a category \mathsf{C}\text{-}\mathsf{Set} of \mathsf{C}-sets and their homomorphisms.
To take an example, we can examine a rule that tells us what happens when we :slice_bread. More precisely, this block of code is constructing a span (\bullet \leftarrow \bullet \rightarrow \bullet) of copresheaves by taking colimits of representable functors. A proof of this statement can be found in (Lane 1978, chap. III.7). The important thing to know is that a representable functor keeps track of all the morphisms that are involved with an object a \in \mathsf{C}, often where the functor is denoted as \mathsf{C}(a,-).
In this code, you can see that there are three objects, I, O, and K, that define an assignment map between things like Knife and knife (note the difference in capitalization).
:slice_bread => @migration(SchDB, begin
I => @join begin
loaf::BreadLoaf
knife::Knife
end
O => @join begin
loaf::BreadLoaf
slice::BreadSlice
food_in_on(bread_slice_is_food(slice)) == food_in_on(bread_loaf_is_food(loaf))
knife::Knife
end
K => @join begin
loaf::BreadLoaf
knife::Knife
end
end),In particular, we can see that for our input we have a functor \texttt{I}: \mathsf{C} \to \mathsf{Set} that sends the objects explicitly as follows: \texttt{BreadLoaf} \mapsto \texttt{loaf} \\ \texttt{Knife} \mapsto \texttt{knife}
The more useful aspect of this functor, however, is the implicit assignment of morphisms and other objects. BreadLoaf and Knife are involved in morphisms in \mathsf{C} whose codomains involve other seemingly hidden objects like Food, Kitchenware, and Entity (described in SchDB). Being a representable functor, I has the important role of accounting for the assignments of these morphisms and objects in the target category, \mathsf{Set}. Because of this, it can be seen that this feature automatically manages implicit inputs (pre-conditions) and outputs (effects) provided the schema sufficiently encoded relationships to other object. This handling of implicit pre-conditions and effects are termed as the qualification problem and the ramification problem of the frame problem, respectively (Ghallab, Nau, and Traverso 2004).
In this category, you also have the ability to glue things together by declaring objects as being equal, as is done in the line:
The gluing can be thought of as a colimit in the category of copresheaves. The result of this particular gluing can be seen below.
Applying rules
Now that we have a sense of how to construct rules, we can see how to use them to derive new world states.
Applicability criteria
As we’ve seen, rules are represented by spans in the category of \mathsf{C}-sets. In the setting of automated planning, we think of these rules as actions in our plan that transform aspects of a world from one state to another. The world state is just another object in our category of copresheaves. In planning, an action can only be applied to the world if the pre-conditions, or inputs, are met in the world state. Therefore, in our framework, we consider a rule to be applicable if there exists a monomorphism from the rule input, I, to the world state in question, Y. The term monomorphism refers to a generalization of an injective function and is denoted by a hooked arrow.
This applicability criteria will be useful in deciding what rules should be considered when building out a task plan.
Mechanics of application
Once we’ve decided that a rule is applicable, how can we use it to induce changes in our world states? Well, we know that the rule is statement about what should be in the world after the rule is applied and what should remain consistent between the input world state and the resulting world state. We also know that the category of copresheaves is an elementary topos, which in particular gives us the freedom to take limits and colimits. This is a convenient fact given that we have been spent much of this exposition talking about spans. So to resolve changes in our world based on a rule, we can consider using the double pushout (DPO) rewriting method (Ehrig, Pfender, and Schneider 1973; Brown et al. 2022).
The general procedure of DPO rewriting is
- Find a pushout complement*
- Complete the left pushout
- Complete the right pushout
*A few notes on pushout complements: A pushout complement is a map that manages the deletion of entities that form the complement K / I. Because i is a monomorphism, the pushout complement is unique up to isomorphism, if it exists. Extra conditions, the identification and dangling conditions, are needed to ensure that the pushout complement exists.
Finding the map f: I \hookrightarrow X that gives the match of the rule to the world state is done using backtracking search. More information about this procedure can be found in the Catlab documentation on finding \mathsf{C}-set homomorphisms.
We can demonstrate what this might look like using our :slice_bread rule and our chosen world state (a well-equipped kitchen!) in the following cartoon.
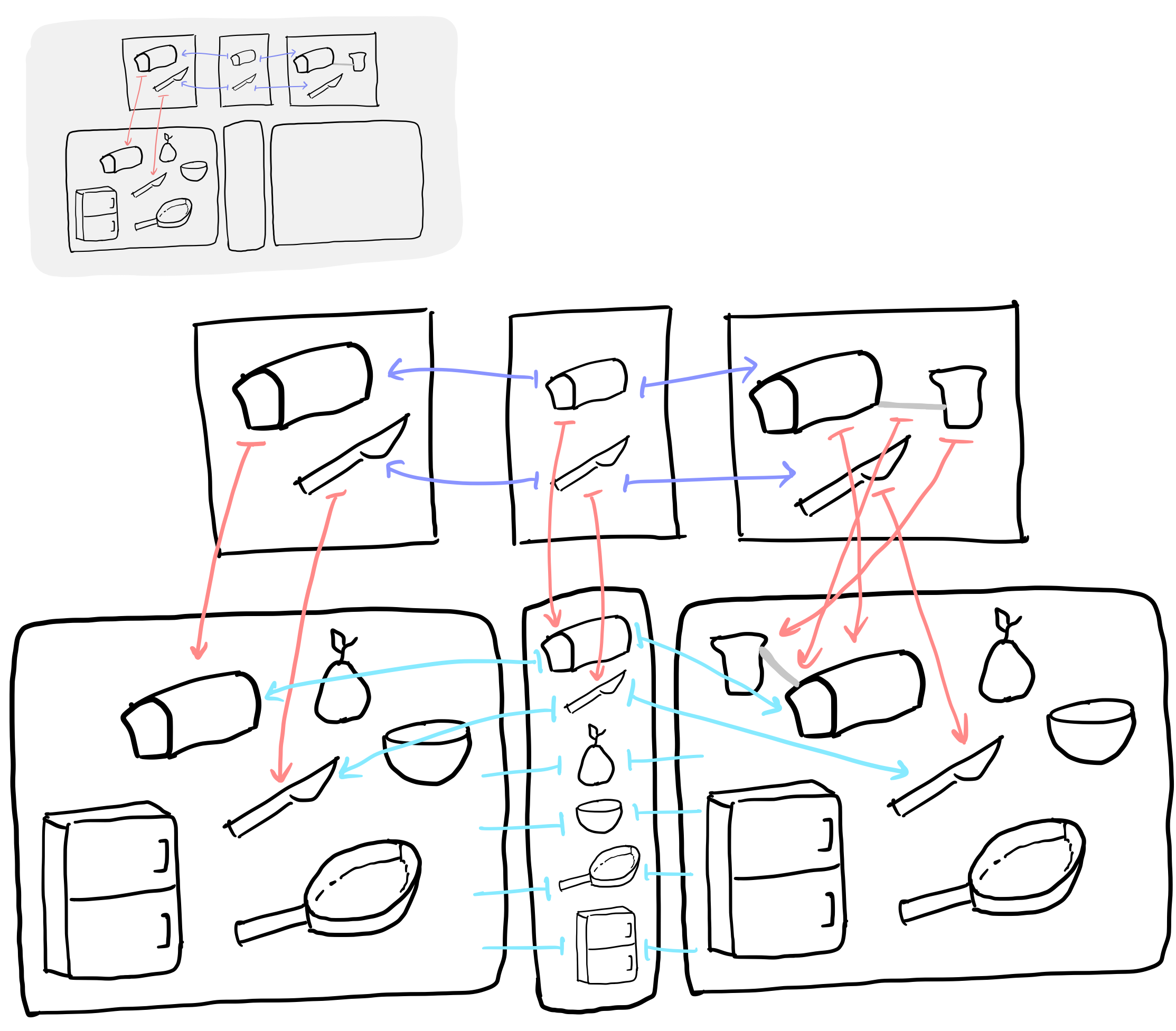
You can see, in the top-left, a depiction of the information we have about our world and our rule. In our world, we have a refridgerator, a loaf of bread, a pear (?), a knife, a bowl, and a skillet. We want to take the action of :slice_bread. Using DPO, we can first identify a map from the rule-keep and the world-keep that is the pushout complement. Recall that a pushout glues the target objects of the span along its apex. Therefore, we can check that our chosen pushout complement produces our world-input. Once we’ve determined this is valid, we can construct the pushout on the right as normal. From this we get a world where there is now all the same entities with the addition of a slice of bread participating in some relationship (gray line) to the loaf of bread. Note: the abbreviated light blue maps in the image should send each entity to “itself” in the world-input and the world-output.
Time to plan (forward with backtracking)!
Now that we know how to choose rules and apply rules, we can begin planning. Recall that a plan is a sequence of actions that change an initial world state to one that satisfies some goal criteria. To set up a planning problem in our framework, we need to point out two objects in the category of copresheaves that are the initial state and the goal state. We can then consider a plan to be a sequence of rules that when applied to the initial state constructs an object such that a monic map exists from the goal state to that object. We borrow from successful methods in the field of automated planning to implement a forward search algorithm with backtracking (Ghallab, Nau, and Traverso 2004, chap. 4). The exit criteria involves checking whether a monic map exists from the goal into the current world state.
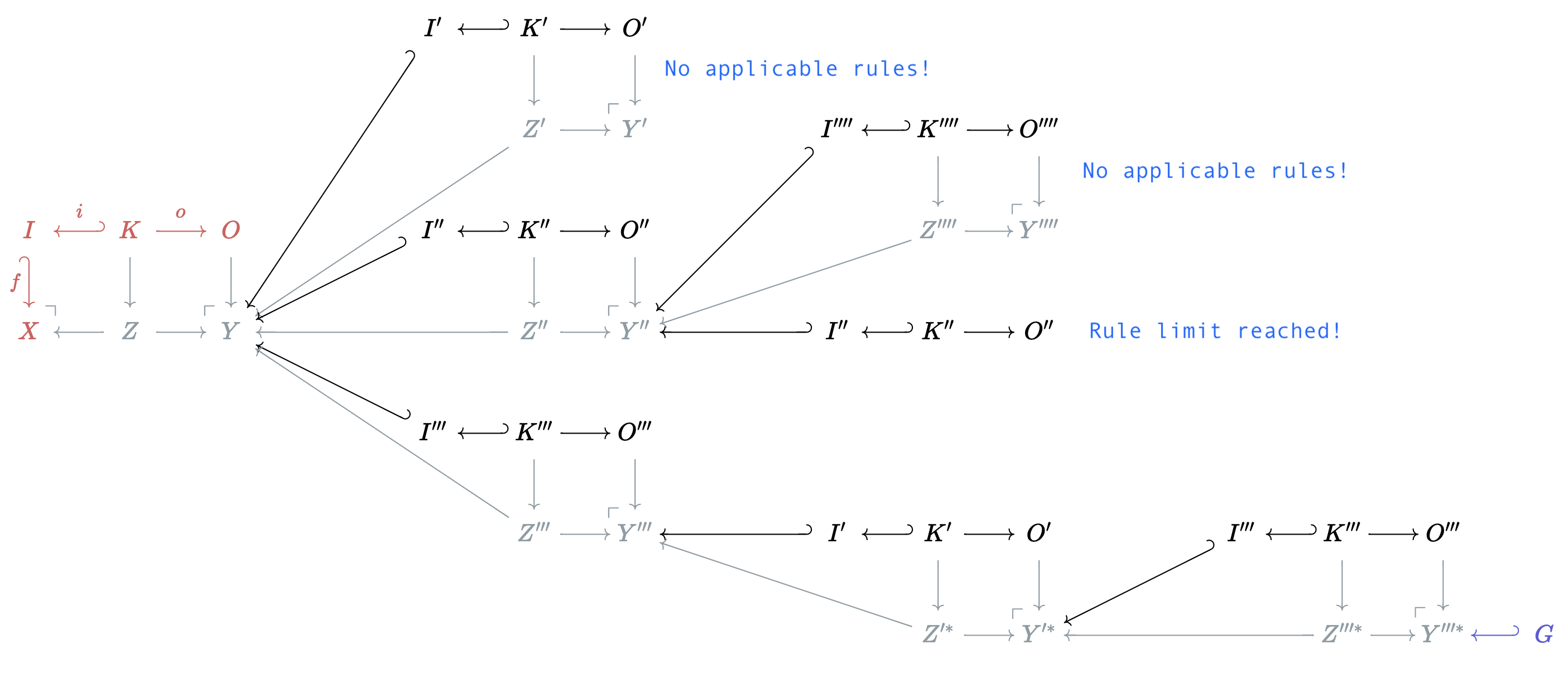
Pseudocode this planning algorithm is as follows:
Algorithm: Forward Planning with Backtracking
Procedure: ForwardPlan(Y world, G goal, r rules, r_usage rule usage, r_limits rule limits, p plan)
(Exit criteria) If monomorphism G \hookrightarrow Y exists
1a. Return Plan
pInitialize applicable rules list,
applicableFor
ruleinrdo3a. Get the input object of
rule, r_I3b. Check if monomorphism r_I \hookrightarrow Y exists
3c. If exists, append
ruletoapplicable(Backtrack criteria) If
applicableis empty, “No applicable rules!” ThrowExceptionFor
ainapplicabledo5a. (Backtrack criteria) If
r_usage[a]>=r_limits[a], “Rule limit reached!” continue5b. Y = DPO(Y, representable(
a))5c. Append
atop5d. ForwardPlan(Y, G,
r,r_usage,r_limits,p)
The deliberate type-setting choice is made to show what data is mathematically rigorous, those in math notation, and what data is a heuristic or workaround not derived from the categorical formalism, those in verbatim font. In particular, we say that Y, G, and r_I are objects in the category of copresheaves.
As with other planning algorithms, this method is subject to issues related to cycles and non-termination. This occurs in scenarios where a rule might be applicable indefinitely if the world specification does not capture a way of destructing an object when a rule is applied. For example, in the present model, slicing the bread does not reduce the bread loaf in any manner which means our planner could potentially slice the bread loaf infinitely many times. The integration of attributed \mathsf{C}-sets, or “acsets”, is in the future of this framework which would allow users to specify attributes for each entity, such as \texttt{BreadLoaf} \to \texttt{NumSlices}. This structure would provide a well-defined way to do arithmetic and other manipulations with the attributes which could help keep track of resource limits. For now, we use an ad hoc method, a rule_limit dictionary that specifies the maximum number of times a rule can be applied in a plan.
Why the categorical abstraction?
You might be wondering what are the benefits of all this formalism when there already exist working systems for automated planning. In fact, the current practice suffers from a number of limitations that I think a categorical point of view can help address.
- A method for propagating implicit pre-conditions and effects. As mentioned earlier, the frame problem is concerned with accounting for implicit world conditions in light of explicit ones. And, as we saw, tracking implicit effects (the so-called ramification problem) and implicit preconditions (the qualification problem) is taken care of because of our use of functors from \mathsf{C} to Set. This gives rule designers to freedom to only model the changes are most important and trust that related changes will be dragged along.
- A common abstraction for actions and events. Existing planners are not able to handle external events. In this framework, actions and events are things of the same type, namely rewrite rules for categorical databases. This means that we can support two modes of operation within a dynamic planning environment: we can (a) apply a rewrite rule that captures some external event and update our current state of the world, or we can (b) search for a plan between the current world state and the goal. This shared abstraction gives us the ability to take in new information and conduct planning without having to state a new planning problem.
- A more structured language than first-order logic. For practioners trying to use automated planning in applications, expressing your planning problem in terms of first-order logic formulas may feel awkward and unstructured. The propositional atoms that comprise these formulas require careful modeling of the semantics with little guidance. For example, some example atoms could be
breadloaf_on_table=True,slice_on_table=False, andknife_in_hand=True; however, they could also bebreadloaf_sitting_on_table=Trueandknife_in_left_hand=Truewhich could serve an equivalent purpose depending on how my actions use these atoms. The ability to capture knowledge under the guidance of an ontology, or schema, provides a more natural way of expressing conditions of the world for planning problems. - A way to handle hierarchy and concurrency. There is currently no way to handle equivalences between permutations of actions that are independent of each other. Forward and backward planning assume totally ordered sequence of actions. Plan-space planning allows a partially ordered set of plans, but does not handle actions that depend on one another. Current planners also do not have ways of dealing with simultaneously occurring actions (Brachman and Levesque 2004, sec. 15.3.1). Expressing a plan, planner, and planning problem using a categorical lanugage would provide a gateway to other structures like operads (hierarchy) and monoidal categories (concurrency).
Despite these benefits, significant work for us remains. This post described a way of stating a planning problem in a categorical way and adapting an existing planning algorithm to work with this abstraction. However, we have still not explained how to describe a plan in a more structured way, beyond just a sequence of rules. Furthermore, we would like to investigate how category theory could help in devising planning algorithms, in particular hierarchical planners. If you have any ideas, please feel free to share your thoughts below!